ĘĮ│╠Ą─ėąĻP(gu©Īn)Ė┼─Ņ
1. ĘĮ│╠Ż║
║¼ėą╬┤ų¬öĄ(sh©┤)Ą─Ą╚╩ĮŠ═Įąū÷ĘĮ│╠����ĪŻ
2. ę╗į¬ę╗┤╬ĘĮ│╠Ż║
ų╗║¼ėąę╗éĆ(g©©)╬┤ų¬öĄ(sh©┤)(į¬)x��Ż¼╬┤ų¬öĄ(sh©┤)xĄ─ųĖöĄ(sh©┤)Č╝╩Ū1(┤╬)����Ż¼▀@śėĄ─ĘĮ│╠Įąū÷ę╗į¬ę╗┤╬ĘĮ│╠�ĪŻ
└²╚ńŻ║ 1700+50x=1800Ż¼ 2(x+1.5x)=5Ą╚Č╝╩Ūę╗į¬ę╗┤╬ĘĮ│╠�����ĪŻ
3Ż«ĘĮ│╠Ą─ĮŌŻ║
╩╣ĘĮ│╠ųąĄ╚╠¢ū¾ėęā╔▀ģŽÓĄ╚Ą─╬┤ų¬öĄ(sh©┤)Ą─ųĄ�Ż¼Įąū÷ĘĮ│╠Ą─ĮŌĪŻ
ūóŻ║
(1) ĘĮ│╠Ą─ĮŌ║═ĮŌĘĮ│╠╩Ū▓╗═¼Ą─Ė┼─ŅŻ¼ĘĮ│╠Ą─ĮŌīŹ(sh©¬)┘|(zh©¼)╔Ž╩ŪŪ¾Ą├Ą─ĮY(ji©”)╣¹�����Ż¼╦³╩Ūę╗éĆ(g©©)öĄ(sh©┤)ųĄ(╗“ÄūéĆ(g©©)öĄ(sh©┤)ųĄ)���Ż¼Č°ĮŌĘĮ│╠Ą─║¼┴x╩ŪųĖŪ¾│÷ĘĮ│╠Ą─ĮŌ╗“┼ąöÓĘĮ│╠¤oĮŌĄ─▀^│╠��ĪŻ
(2)ĘĮ│╠Ą─ĮŌĄ─Öz“×(y©żn)ĘĮĘ©�Ż¼╩ūŽ╚░č╬┤ų¬öĄ(sh©┤)Ą─ųĄĘųäe┤·╚ļĘĮ│╠Ą─ū¾����Īóėęā╔▀ģėŗ(j©¼)╦Ń╦³éāĄ─ųĄŻ¼Ųõ┤╬▒╚▌^ā╔▀ģĄ─ųĄ╩ŪʱŽÓĄ╚Å─Č°Ą├│÷ĮY(ji©”)šō�ĪŻ
Ą╚╩ĮĄ─ąį┘|(zh©¼)
Ą╚╩ĮĄ─ąį┘|(zh©¼)(1)Ż║
Ą╚╩Įā╔▀ģČ╝╝ė╔Ž(╗“£p╚ź)═¼éĆ(g©©)öĄ(sh©┤)(╗“╩Įūė)Ż¼ĮY(ji©”)╣¹╚įŽÓĄ╚�����ĪŻ
ė├╩Įūėą╬╩Į▒Ē╩Š×ķŻ║╚ń╣¹a=b���Ż¼─Ū├┤a±c=b±c
Ą╚╩ĮĄ─ąį┘|(zh©¼)(2)Ż║
Ą╚╩Įā╔▀ģ│╦═¼ę╗éĆ(g©©)öĄ(sh©┤)���Ż¼╗“│²ęį═¼ę╗éĆ(g©©)▓╗×ķ0Ą─öĄ(sh©┤)Ż¼ĮY(ji©”)╣¹╚įŽÓĄ╚Ż¼ė├╩Įūėą╬╩Į▒Ē╩Š×ķŻ║╚ń╣¹a=b����Ż¼─Ū├┤ac=bc;╚ń╣¹a=b(c≠0)Ż¼─Ū├┤a/c=b/c���ĪŻ
ęŲĒŚ(xi©żng)Ę©ät
░čĄ╚╩Įę╗▀ģĄ──│ĒŚ(xi©żng)ūā╠¢║¾ęŲĄĮ┴Ēę╗▀ģ��Ż¼Įąū÷ęŲĒŚ(xi©żng)�����ĪŻ
╚ź└©╠¢Ę©ät
1. └©╠¢═ŌĄ─ę“öĄ(sh©┤)╩Ūš²öĄ(sh©┤)��Ż¼╚ź└©╠¢║¾Ė„ĒŚ(xi©żng)Ą─Ę¹╠¢┼cįŁ└©╠¢ā╚(n©©i)ŽÓæ¬(y©®ng)Ė„ĒŚ(xi©żng)Ą─Ę¹╠¢ŽÓ═¼�����ĪŻ
2. └©╠¢═ŌĄ─ę“öĄ(sh©┤)╩Ūžō(f©┤)öĄ(sh©┤)Ż¼╚ź└©╠¢║¾Ė„ĒŚ(xi©żng)Ą─Ę¹╠¢┼cįŁ└©╠¢ā╚(n©©i)ŽÓæ¬(y©®ng)Ė„ĒŚ(xi©żng)Ą─Ę¹╠¢Ė─ūā��ĪŻ
ĮŌĘĮ│╠Ą─ę╗░Ń▓Į¾E
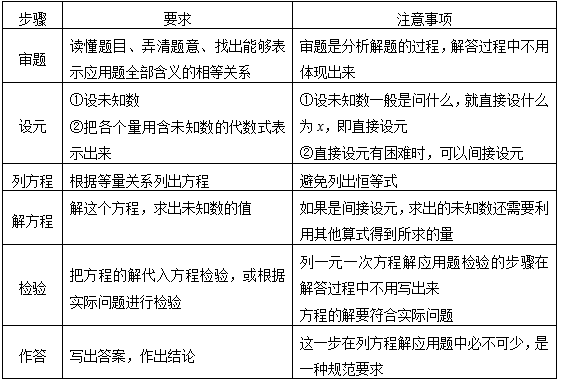
1. ╚źĘų─Ė(ĘĮ│╠ā╔▀ģ═¼│╦Ė„Ęų─ĖĄ─ūŅąĪ╣½▒ČöĄ(sh©┤))
2. ╚ź└©╠¢(░┤╚ź└©╠¢Ę©ät║═Ęų┼õ┬╔)
3. ęŲĒŚ(xi©żng)(░č║¼ėą╬┤ų¬öĄ(sh©┤)Ą─ĒŚ(xi©żng)ęŲĄĮĘĮ│╠ę╗▀ģ����Ż¼Ųõ╦¹ĒŚ(xi©żng)Č╝ęŲĄĮĘĮ│╠Ą─┴Ēę╗▀ģŻ¼ęŲĒŚ(xi©żng)ę¬ūā╠¢)
4. ║Ž▓ó(░čĘĮ│╠╗»│╔ax = b (a≠0)ą╬╩Į)
5. ŽĄöĄ(sh©┤)╗»×ķ1(į┌ĘĮ│╠ā╔▀ģČ╝│²ęį╬┤ų¬öĄ(sh©┤)Ą─ŽĄöĄ(sh©┤)aŻ¼Ą├ĄĮĘĮ│╠Ą─ĮŌx=).
┴ąę╗į¬ę╗┤╬ĘĮ│╠ĮŌæ¬(y©®ng)ė├Ņ}Ą─ę╗░Ń▓Į¾E
1.┴ąĘĮ│╠ĮŌæ¬(y©®ng)ė├Ņ}Ą─╗∙▒Š▓Į¾E
ūóęŌŻ║
(1)│§ųą┴ąĘĮ│╠ĮŌæ¬(y©®ng)ė├Ņ}Ģr(sh©¬)�����Ż¼į§├┤┴ą║åå╬Š═į§├┤┴ą(╝┤╦∙┴ąĄ─├┐ę╗éĆ(g©©)ĘĮ│╠Č╝ų▒ĮėĄ─▒Ē╩ŠŅ}ęŌ)�Ż¼▓╗ė├ō·(d©Īn)ą─╬┤ų¬öĄ(sh©┤)▀^ČÓŻ¼║å╗»īÅŅ}║═┴ąĘĮ│╠Ą─▓Į¾E�����Ż¼░čļyČ╚▐D(zhu©Żn)ęŲĄĮĮŌĘĮ│╠Ą─▓Į¾E╔Ž�����ĪŻ
(2)ĮŌĘĮ│╠Ą─▓Į¾E▓╗ė├īæ│÷���Ż¼ų▒ĮėīæĮY(ji©”)╣¹╝┤┐╔����ĪŻ
(3)įO(sh©©)╬┤ų¬öĄ(sh©┤)Ģr(sh©¬)����Ż¼ę¬ś╦(bi©Īo)├„å╬╬╗Ż¼į┌┴ąĘĮ│╠Ģr(sh©¬)����Ż¼╚ń╣¹Ņ}ųąöĄ(sh©┤)ō■(j©┤)Ą─å╬╬╗▓╗Įy(t©»ng)ę╗���Ż¼▒žĒÜ░čå╬╬╗ōQ╦Ń│╔Įy(t©»ng)ę╗å╬╬╗Ż¼ė╚Ųõ╩Ūąą│╠å¢Ņ}└’ąĶę¬ūóęŌ▀@éĆ(g©©)å¢Ņ}�����ĪŻ
2.įO(sh©©)╬┤ų¬öĄ(sh©┤)Ą─ĘĮĘ©
įO(sh©©)╬┤ų¬öĄ(sh©┤)Ą─ĘĮĘ©ę╗░ŃüĒųv���Ż¼ėąęįŽ┬ÄūĘNŻ║
(1)“ų▒ĮėįO(sh©©)į¬”Ż║Ņ}─┐└’ę¬Ū¾Ą─╬┤ų¬┴┐╩Ū╩▓├┤�Ż¼Š═░č╦³įO(sh©©)×ķ╬┤ų¬öĄ(sh©┤)����Ż¼ČÓ▀mė├ė┌ę¬Ū¾Ą─╬┤ų¬öĄ(sh©┤)ų╗ėąę╗éĆ(g©©)Ą─ŪķørĪŻ
(2)“ķgĮėįO(sh©©)į¬”Ż║ėąą®æ¬(y©®ng)ė├Ņ}���Ż¼╚¶ų▒ĮėįO(sh©©)╬┤ų¬öĄ(sh©┤)║▄ļy┴ą│÷ĘĮ│╠�Ż¼╗“š▀╦∙┴ąĄ─ĘĮ│╠▒╚▌^Å═(f©┤)ļs��Ż¼┐╔ęį▀xō±ķgĮėįO(sh©©)╬┤ų¬öĄ(sh©┤)����Ż¼Č°ĮŌĄ├Ą─ķgĮė╬┤ų¬öĄ(sh©┤)ī”┤_Č©╦∙Ū¾Ą─┴┐ŲųąĮķū„ė├ĪŻ
(3)“▌oų·įO(sh©©)į¬”Ż║ėąą®æ¬(y©®ng)ė├Ņ}▓╗āHę¬ų▒ĮėįO(sh©©)╬┤ų¬öĄ(sh©┤)����Ż¼Č°Ūęę¬į÷╝ė▌oų·╬┤ų¬öĄ(sh©┤)Ż¼Ą½▀@ą®▌oų·╬┤ų¬öĄ(sh©┤)▒Š╔Ē▓ó▓╗ąĶę¬Ū¾│÷���Ż¼╦³éāĄ─ū„ė├ų╗╩Ū×ķ┴╦Ä═ų·┴ąĘĮ│╠���Ż¼═¼Ģr(sh©¬)×ķ┴╦Ū¾│÷šµš²Ą─╬┤ų¬┴┐Ż¼┐╔ęįį┌ĮŌŅ}Ģr(sh©¬)Ž¹╚ź�����ĪŻ
(4)“▓┐ĘųįO(sh©©)į¬”┼c“š¹¾wįO(sh©©)į¬”▐D(zhu©Żn)ōQŻ║«ö(d©Īng)š¹¾wįO(sh©©)į¬ėą└¦ļyĢr(sh©¬)�Ż¼┐╔ęį┐╝æ]įO(sh©©)Ųõę╗▓┐Ęų×ķ╬┤ų¬öĄ(sh©┤)Ż¼Ę┤ų«ęÓ╚╗�Ż¼╚ńŻ║öĄ(sh©┤)ūųå¢Ņ}ĪŻ
' fill='%23FFFFFF'%3E%3Crect x='249' y='126' width='1' height='1'%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
Ņ}ą═ę╗Ż║öĄ(sh©┤)ūųå¢Ņ}
(1)ČÓ╬╗öĄ(sh©┤)ūųĄ─▒Ē╩ŠĘĮĘ©Ż║
ę╗éĆ(g©©)ā╔╬╗öĄ(sh©┤)Ą─╩«╬╗öĄ(sh©┤)ūų�����ĪóéĆ(g©©)╬╗öĄ(sh©┤)ūųĘųäe×ķa��Īób���Ż¼(Ųõųąa����ĪóbŠ∙×ķš¹öĄ(sh©┤)Ż¼ 1≤a≤9��Ż¼0≤b≤9)ät▀@éĆ(g©©)ā╔╬╗öĄ(sh©┤)┐╔ęį▒Ē╩Š×ķ10a+b
ę╗éĆ(g©©)╚²╬╗öĄ(sh©┤)Ą─░┘╬╗öĄ(sh©┤)ūų×ķa�Ż¼╩«╬╗öĄ(sh©┤)ūų×ķbŻ¼éĆ(g©©)╬╗öĄ(sh©┤)ūų×ķc���Ż¼(ŲõųąŠ∙×ķš¹öĄ(sh©┤)���Ż¼Ūę1≤a≤9Ż¼0≤b≤9�����Ż¼0≤c≤9)ät▀@éĆ(g©©)╚²╬╗öĄ(sh©┤)▒Ē╩Š×ķŻ║100a+b+c
(2)ŲµöĄ(sh©┤)┼c┼╝öĄ(sh©┤)Ą─▒Ē╩ŠĘĮĘ©Ż║
┼╝öĄ(sh©┤)┐╔▒Ē╩Š×ķ2k���Ż¼ŲµöĄ(sh©┤)┐╔▒Ē╩Š×ķ2k+1(Ųõųąk▒Ē╩Šš¹öĄ(sh©┤))
(3)╚²éĆ(g©©)ŽÓÓÅĄ─š¹öĄ(sh©┤)Ą─▒Ē╩ŠĘĮĘ©Ż║
┐╔įO(sh©©)ųąķgę╗éĆ(g©©)š¹öĄ(sh©┤)×ķa����Ż¼ät▀@╚²éĆ(g©©)ŽÓÓÅĄ─š¹öĄ(sh©┤)┐╔▒Ē╩Š×ķa-1,a,a+1��ĪŻ
└²1Ż║ę╗┤╬öĄ(sh©┤)īW(xu©”)£y“×(y©żn)ųą����Ż¼ąĪ├„šJ(r©©n)×ķūį╝║┐╔ęįĄ├ØMĘųŻ¼▓╗┴ŽŠĒūė░l(f©Ī)Ž┬üĒę╗┐┤Ą├┴╦96Ęų�����Ż¼įŁüĒ╩Ūė╔ė┌┤ųą─░čę╗éĆ(g©©)Ņ}─┐Ą─┤░Ė╩«╬╗┼céĆ(g©©)╬╗öĄ(sh©┤)ūųīæŅŹĄ╣┴╦���Ż¼ĮY(ji©”)╣¹ūį╝║Ą─┤░Ė▒╚š²┤_┤░Ė┤¾┴╦36�Ż¼Č°š²┤_┤░ĖĄ─éĆ(g©©)╬╗öĄ(sh©┤)ūų╩Ū╩«╬╗öĄ(sh©┤)ūųĄ─2▒Č.š²┤_┤░Ė╩ŪČÓ╔┘?
└²2Ż║─│─ĻĘ▌Ą─╠¢┤a╩Ūę╗éĆ(g©©)╦─╬╗öĄ(sh©┤)����Ż¼╦³Ą─Ū¦╬╗öĄ(sh©┤)ūų╩Ū2Ż¼╚ń╣¹░č2ęŲĄĮéĆ(g©©)╬╗╔Ž╚ź����Ż¼─Ū├┤╦∙Ą├Ą─ą┬╦─╬╗öĄ(sh©┤)▒╚įŁ╦─╬╗öĄ(sh©┤)Ą─2▒Č╔┘6Ż¼Ū¾▀@éĆ(g©©)─ĻĘ▌����ĪŻ
Ņ}ą═Č■Ż║╚šÜvå¢Ņ}
(1)į┌╚šÜvå¢Ņ}ųąŻ¼ÖMąąŽÓÓÅā╔öĄ(sh©┤)ŽÓ▓Ņ1�����Ż¼žQ┴ąŽÓÓÅā╔öĄ(sh©┤)ŽÓ▓Ņ7.
(2)╚šÜvųąę╗éĆ(g©©)žQ┴ą╔ŽŽÓÓÅ3éĆ(g©©)öĄ(sh©┤)Ą─║═Ą─ūŅąĪųĄĢr(sh©¬)24Ż¼ūŅ┤¾ųĄĢr(sh©¬)72����Ż¼Ūę▀@éĆ(g©©)║═ę╗Č©╩Ū3Ą─▒ČöĄ(sh©┤).
(3)ę╗─ĻųąŻ¼├┐į┬Ą─╠ņöĄ(sh©┤)╩ŪėąęÄ(gu©®)┬╔Ą─���Ż¼ę╗����Īó╚²�����Īó╬Õ����ĪóŲ▀Īó░╦�Īó╩«Īó╩«Č■▀@Ų▀éĆ(g©©)į┬├┐į┬Č╝╩Ū31╠ņ�Ż¼╦─Īó┴∙ĪóŠ┼�Īó╩«ę╗▀@╦─éĆ(g©©)į┬├┐į┬Č╝╩Ū30╠ņŻ¼Č■į┬ŲĮ─Ļ28╠ņ���Ż¼ķc─Ļ29╠ņ��Ż¼╦∙ęįŻ¼╚šÜv▒Ēųą╚šŲ┌Ą─╚ĪųĄ╩ŪėąĘČć·Ą─.
└²3Ż║Ž┬▒Ē╩Ū2011─Ļ12į┬Ą─╚šÜv▒Ē����Ż¼šłĮŌ┤å¢Ņ}Ż║į┌▒Ēųąė├ą╬╚ńŽ┬łDĄ─ŲĮąą╦─▀ģą╬┐“┐“│÷4éĆ(g©©)öĄ(sh©┤)Ż¼
(1)╚¶┐“│÷Ą─4éĆ(g©©)öĄ(sh©┤)Ą─║═×ķ74��Ż¼šł─Ń═©▀^┴ąĘĮ│╠Ą─▐kĘ©�Ż¼Ū¾│÷╦³Ęųäe╩Ū──4╠ņ?
(2)┐“│÷Ą─4éĆ(g©©)öĄ(sh©┤)Ą─║═┐╔─▄╩Ū26åß?×ķ╩▓├┤?

└²4Ż║╚ńłDŻ¼┐“ā╚(n©©i)Ą─╦─éĆ(g©©)öĄ(sh©┤)ūųĄ─║═×ķ28�Ż¼šł═©▀^ŲĮęŲķLĘĮą╬┐“Ą─ĘĮĘ©Ż¼╩╣┐“ā╚(n©©i)Ą─öĄ(sh©┤)ūųų«║═×ķ68���Ż¼▀@śėĄ─ķLĘĮą╬Ą─╬╗ų├ėąÄūéĆ(g©©)?─▄ʱ╩╣┐“ā╚(n©©i)Ą─╦─éĆ(g©©)öĄ(sh©┤)ūųų«║═×ķ49?╚¶─▄��Ż¼šłšę│÷▀@śėĄ─╬╗ų├;╚¶▓╗─▄���Ż¼šłšf├„└Ēė╔.
' fill='%23FFFFFF'%3E%3Crect x='249' y='126' width='1' height='1'%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
Ņ}ą═╚²Ż║║═▓Ņ▒ČĘųå¢Ņ}
║═Īó▓ŅĪó▒Čå¢Ņ}ĻP(gu©Īn)µIę¬ĘųŪÕ╩ŪÄū▒ČČÓÄū║═Äū▒Č╔┘Äū.
(1)«ö(d©Īng)▌^┤¾┴┐╩Ū▌^ąĪ┴┐Ą─Äū▒ČČÓÄūĢr(sh©¬)
(2)«ö(d©Īng)▌^┤¾┴┐╩Ū▌^ąĪ┴┐Ą─Äū▒Č╔┘ÄūĢr(sh©¬)
└²5Ż║ę╗▓┐═Ž└ŁÖC(j©®)Ė¹ę╗Ų¼Ąž���Ż¼Ą┌ę╗╠ņĖ¹┴╦▀@Ų¼ĄžĄ─;Ą┌Č■╠ņĖ¹┴╦╩ŻŽ┬▓┐ĘųĄ─��Ż¼▀Ć╩ŻŽ┬42╣½ĒĢø]Ė¹═Ļ���Ż¼ät▀@Ų¼Ąž╣▓ėąČÓ╔┘╣½ĒĢ?
└²6Ż║─┴č“╚╦┌sų°ę╗╚║č“?q©▒)żšęę╗éĆ(g©©)▓▌ķLĄ├├»╩óĄ─ĄžĘĮŻ¼ę╗éĆ(g©©)▀^┬Ę╚╦Ā┐ų°ę╗ų╗Ę╩č“Å─║¾├µĖ·┴╦╔ŽüĒ�Ż¼╦¹ī”─┴č“╚╦šfŻ║“─Ń┌sĄ─▀@╚║č“┤¾Ė┼ėą100ų╗░╔!”─┴č“╚╦┤Ą└Ż║“╚ń╣¹▀@╚║č“į÷╝ėę╗▒ČŻ¼į┘╝ė╔ŽįŁüĒ▀@╚║č“Ą─ę╗░ļ���Ż¼ėų╝ė╔ŽįŁüĒ▀@╚║č“ę╗░ļĄ─ę╗░ļ��Ż¼▀B─Ń▀@ų╗č“ę▓╦Ń▀M(j©¼n)╚ź�Ż¼▓┼äé║├£ÉØM100ų╗.”å¢─┴č“╚╦Ą─▀@╚║č“╣▓ėąČÓ╔┘ų╗?
Ņ}ą═╦─Ż║ąą│╠å¢Ņ}
1.ąą│╠å¢Ņ}
┬Ę│╠=╦┘Č╚×Ģr(sh©¬)ķg
ŽÓė÷┬Ę│╠=╦┘Č╚║═׎Óė÷Ģr(sh©¬)ķg
ūĘ╝░┬Ę│╠=╦┘Č╚▓Ņ×ūĘ╝░Ģr(sh©¬)ķg
2.┴„╦«ąą┤¼å¢Ņ}
Ēś┴„╦┘Č╚=ņo╦«╦┘Č╚+╦«┴„╦┘Č╚
─µ┴„╦┘Č╚=ņo╦«╦┘Č╚-╦«┴„╦┘Č╚
╦«┴„╦┘Č╚=×(Ēś┴„╦┘Č╚-─µ┴„╦┘Č╚)
3.╗▄ć▀^ś“å¢Ņ}
╗▄ć▀^ś“å¢Ņ}╩Ūę╗ĘN╠ž╩ŌĄ─ąą│╠å¢Ņ}����Ż¼ąĶę¬ūóęŌÅ─▄ćŅ^ų┴ś“ŲŻ¼ĄĮ▄ć╬▓ļxś“ų╣��Ż¼╗▄ć╦∙ąąŠÓļxĄ╚ė┌ś“ķL╝ė╔Ž▄ćķL���Ż¼┴ą▄ć▀^ś“å¢Ņ}Ą─╗∙▒ŠöĄ(sh©┤)┴┐ĻP(gu©Īn)ŽĄ×ķŻ║
▄ć╦┘×▀^ś“Ģr(sh©¬)ķg=▄ćķL+ś“ķL.
└²7Ż║ėą╝ū��Īóęę�����Īó▒¹╚²╚╦═¼Ģr(sh©¬)═¼Ąž│÷░l(f©Ī)�Ż¼└@ę╗éĆ(g©©)╗©Ųįąąū▀Ż¼ęę�����Īó▒¹Č■╚╦═¼ĘĮŽ“ąąū▀���Ż¼╝ū┼cęęĪó▒¹▒│Ž“Č°ąą.╝ū├┐ĘųńŖū▀40├ū����Ż¼ęę├┐ĘųńŖū▀38├ūŻ¼▒¹├┐ĘųńŖū▀36├ū.│÷░l(f©Ī)║¾�����Ż¼╝ū║═ęęŽÓė÷║¾3ĘųńŖ║═▒¹ŽÓė÷�Ż¼Ū¾╗©ŲįĄ─ų▄ķL.
└²8Ż║─│╚╦Å─╝ę└’“T─”═ą▄ćĄĮ╗▄暊Ż¼╚ń╣¹├┐ąĪĢr(sh©¬)ąą30Ū¦├ū����Ż¼─Ū├┤▒╚╗▄ćķ_▄ćĢr(sh©¬)ķgįńĄĮ15ĘųńŖ���Ż¼╚¶├┐ąĪĢr(sh©¬)ąą18Ū¦├ūŻ¼ät▒╚╗▄ćķ_▄ćĢr(sh©¬)ķg▀tĄĮ15ĘųńŖ�����Ż¼¼F(xi©żn)į┌┤╦╚╦┤“╦Ńį┌╗▄ćķ_▄ćŪ░10ĘųńŖĄĮ▀_(d©ó)╗▄暊��Ż¼ät┤╦╚╦┤╦Ģr(sh©¬)“T─”═ą▄ćĄ─╦┘Č╚æ¬(y©®ng)×ķČÓ╔┘?
└²9Ż║ę╗ąĪ┤¼ė╔AĖ█ĄĮBĖ█Ēś┴„ąĶąą6ąĪĢr(sh©¬)�Ż¼ė╔BĖ█ĄĮAĖ█─µ┴„ąĶąą8ąĪĢr(sh©¬)Ż¼ę╗╠ņ�����Ż¼ąĪ┤¼Å─įń│┐6³c(di©Żn)ė╔AĖ█│÷░l(f©Ī)Ēś┴„ąąų┴BĖ█Ģr(sh©¬)��Ż¼░l(f©Ī)¼F(xi©żn)ę╗Š╚╔·╚”į┌═ŠųąĄ¶┬õį┌╦«ųą����Ż¼┴ó╝┤ĘĄ╗žŻ¼1ąĪĢr(sh©¬)║¾šęĄĮŠ╚╔·╚”.å¢Ż║
(1)╚¶ąĪ┤¼░┤╦«┴„╦┘Č╚ė╔AĖ█Ų»┴„ĄĮBĖ█ąĶČÓ╔┘ąĪĢr(sh©¬)?
(2)Š╚╔·╚”╩Ū║╬Ģr(sh©¬)Ą¶╚ļ╦«ųąĄ─?
Ņ}ą═╬ÕŻ║╣ż│╠å¢Ņ}
╣żū„┐é┴┐=╣żū„Ģr(sh©¬)ķg×╣żū„ą¦┬╩
Ė„▓┐Ęų╣żū„┴┐ų«║═=1
└²10Ż║ėą╝ū����Īóęę���Īó▒¹╚²éĆ(g©©)╦«╣▄Ż¼¬Ü(d©▓)ķ_╝ū╣▄5ąĪĢr(sh©¬)┐╔ęįūóØMę╗│ž╦«;╝ū��Īóęęā╔╣▄²Rķ_���Ż¼2ąĪĢr(sh©¬)┐╔ūóØMę╗│ž╦«;╝ū�Īó▒¹ā╔╣▄²Rķ_�����Ż¼3ąĪĢr(sh©¬)ūóØMę╗│ž╦«.¼F(xi©żn)░č╚²╣▄ę╗²Rķ_�����Ż¼▀^┴╦ę╗Č╬Ģr(sh©¬)ķg║¾╝ū╣▄ę“╣╩šŽ═Żķ_����Ż¼═Żķ_║¾2ąĪĢr(sh©¬)╦«│žūóØM.å¢╚²╣▄²Rķ_┴╦ČÓ╔┘ąĪĢr(sh©¬)?
└²11Ż║Özą▐ę╗ūĪš¼ģ^(q©▒)Ą─ūįüĒ╦«╣▄Ą└���Ż¼╝ūå╬¬Ü(d©▓)═Ļ│╔ąĶ14╠ņ��Ż¼ęęå╬¬Ü(d©▓)═Ļ│╔ąĶ18╠ņ�����Ż¼▒¹å╬¬Ü(d©▓)═Ļ│╔ąĶ12╠ņ.Ū░7╠ņė╔╝ū���Īóęęā╔╚╦║Žū„���Ż¼Ą½ęęųą═Šļxķ_┴╦ę╗Č╬Ģr(sh©¬)ķgŻ¼║¾2╠ņė╔ęę�Īó▒¹ā╔╚╦║Žū„═Ļ│╔Ż¼å¢ęęųą═Šļxķ_┴╦Äū╠ņ?
Ņ}ą═┴∙Ż║╔╠ŲĘõN╩█å¢Ņ}
į┌¼F(xi©żn)īŹ(sh©¬)╔·╗Ņųą����Ż¼┘Å┘I╔╠ŲĘ║═õN╩█╔╠ŲĘĢr(sh©¬)Ż¼Įø(j©®ng)│ŻĢ■ė÷ĄĮ▀M(j©¼n)ār(ji©ż)���Īóś╦(bi©Īo)ār(ji©ż)�����Īó╩█ār(ji©ż)�����Īó┤“š█Ą╚Ė┼─Ņ���Ż¼į┌┴╦ĮŌ▀@ą®╗∙▒ŠĖ┼─ŅĄ─╗∙ĄA(ch©│)╔Ž����Ż¼▀Ć▒žĒÜšŲ╬šęįŽ┬ÄūéĆ(g©©)Ą╚┴┐ĻP(gu©Īn)ŽĄŻ║
└¹ØÖ=╩█ār(ji©ż)-▀M(j©¼n)ār(ji©ż)
└¹ØÖ=▀M(j©¼n)ār(ji©ż)×└¹ØÖ┬╩
īŹ(sh©¬)ļH╩█ār(ji©ż)=ś╦(bi©Īo)ār(ji©ż)×┤“š█┬╩
└²12Ż║─│╔╠ł÷Įø(j©®ng)õNę╗ĘN╔╠ŲĘ�Ż¼ė╔ė┌▀M(j©¼n)žøĢr(sh©¬)ār(ji©ż)Ė±▒╚įŁ▀M(j©¼n)ār(ji©ż)ĮĄĄ═┴╦Ż¼╩╣Ą├└¹ØÖį÷╝ė┴╦8éĆ(g©©)░┘Ęų³c(di©Żn)��Ż¼Ū¾Įø(j©®ng)õN▀@ĘN╔╠ŲĘįŁüĒĄ─└¹ØÖ┬╩�ĪŻ
└²13Ż║─│╔╠ŲĘį┬─®Ą─▀M(j©¼n)žøār(ji©ż)×ķ▒╚į┬│§Ą─▀M(j©¼n)žøār(ji©ż)ĮĄ┴╦8%Ż¼Č°õN╩█ār(ji©ż)▓╗ūā��Ż¼▀@śė����Ż¼└¹ØÖ┬╩į┬─®▒╚į┬│§Ė▀10%Ż¼å¢į┬│§Ą─└¹ØÖ┬╩╩ŪČÓ╔┘?
Ņ}ą═Ų▀Ż║ĘĮ░ĖøQ▓▀å¢Ņ}
į┌īŹ(sh©¬)ļH╔·╗Ņųą��Ż¼ū÷ę╗╝■╩┬Ūķ═∙═∙Ģ■ėąČÓĘN▀xō±�Ż¼▀@Š═ąĶę¬Å─ÄūĘNĘĮ░Ėųą���Ż¼▀xō±ūŅ╝čĘĮ░Ė���Ż¼╚ńŠW(w©Żng)Įj(lu©░)Ą─╩╣ė├��Ż¼ĄĮ▓╗═¼┬├ąą╔ń┘ÅŲ▒Ą╚���Ż¼ę╗░ŃČ╝ę¬▀\(y©┤n)ė├ĘĮ│╠ĮŌ┤Ż¼░č├┐ę╗ĘNĘĮ░ĖĄ─ĮY(ji©”)╣¹Ž╚╦Ń│÷üĒ�����Ż¼▀M(j©¼n)ąą▒╚▌^║¾Ą├│÷ūŅ╝čĘĮ░Ė�ĪŻ
└²14Ż║─│ķ_░l(f©Ī)╔╠▀M(j©¼n)ąą╔╠õü┤┘õNŻ¼ÅVĖµ╔Žīæų°╚ńŽ┬Śl┐ŅŻ║
═Č┘Yš▀┘Å┘I╔╠õü║¾�����Ż¼▒žĒÜė╔ķ_░l(f©Ī)╔╠┤·×ķūŌ┘U5─Ļ�����Ż¼5─ĻŲ┌ØM║¾ė╔ķ_░l(f©Ī)╔╠ęį▒╚įŁ╔╠õüś╦(bi©Īo)ār(ji©ż)Ė▀20%Ą─ār(ji©ż)Ė±▀M(j©¼n)ąą╗ž┘Å����Ż¼═Č┘Yš▀┐╔į┌ęįŽ┬ā╔ĘN┘ÅõüĘĮ░Ėųąū÷│÷▀xō±Ż║
ĘĮ░Ėę╗Ż║═Č┘Yš▀░┤╔╠õüś╦(bi©Īo)ār(ji©ż)ę╗┤╬ąįĖČŪÕõü┐ŅŻ¼├┐─Ļ┐╔ęį½@Ą├Ą─ūŌĮ×ķ╔╠õüś╦(bi©Īo)ār(ji©ż)Ą─10%.
ĘĮ░ĖČ■Ż║═Č┘Yš▀░┤╔╠õüś╦(bi©Īo)ār(ji©ż)Ą─░╦╬Õš█ę╗┤╬ąįĖČŪÕõü┐Ņ�����Ż¼2─Ļ║¾├┐─Ļ┐╔ęį½@Ą├Ą─ūŌĮ×ķ╔╠õüś╦(bi©Īo)ār(ji©ż)Ą─10%Ż¼Ą½ę¬└U╝{ūŌĮĄ─10%ū„×ķ╣▄└Ē┘M(f©©i)ė├.
(1)šłå¢Ż║═Č┘Yš▀▀xō±──ĘN┘ÅõüĘĮ░Ė�����Ż¼5─Ļ║¾╦∙½@Ą├Ą─═Č┘Y╩šęµ┬╩Ė³Ė▀?×ķ╩▓├┤?(ūóŻ║)
(2)ī”═¼ę╗ś╦(bi©Īo)ār(ji©ż)Ą─╔╠õü���Ż¼╝ū▀xō±┴╦┘ÅõüĘĮ░Ėę╗�����Ż¼ęę▀xō±┴╦┘ÅõüĘĮ░ĖČ■�����Ż¼─Ū├┤5─Ļ║¾ā╔╚╦½@Ą├Ą─╩šęµīóŽÓ▓Ņ5╚fį¬.å¢Ż║╝ū�Īóęęā╔╚╦Ė„═Č┘Y┴╦ČÓ╔┘╚fį¬?
└²15Ż║ėąę╗éĆ(g©©)ų╗į╩įSå╬Ž“═©▀^Ą─šŁĄ└┐┌����Ż¼═©│ŻŪķørŽ┬Ż¼├┐ĘųńŖ┐╔ęį═©▀^9╚╦.ę╗╠ņ═§└ŽÄ¤ĄĮ▀_(d©ó)Ą└┐┌Ģr(sh©¬)��Ż¼░l(f©Ī)¼F(xi©żn)ė╔ė┌ōĒöD����Ż¼├┐ĘųńŖų╗─▄ėą3╚╦═©▀^Ą└┐┌Ż¼┤╦Ģr(sh©¬)�Ż¼ūį╝║Ū░├µ▀Ćėą36éĆ(g©©)╚╦Ą╚┤²═©▀^Ż¼═©▀^Ą└┐┌║¾���Ż¼▀ĆąĶ7ĘųńŖĄĮ▀_(d©ó)īW(xu©”)ąŻ.
(1)╚¶└@Ą└Č°ąą���Ż¼ę¬15ĘųńŖĄĮ▀_(d©ó)īW(xu©”)ąŻĪŻÅ─╣Ø(ji©”)╩ĪĢr(sh©¬)ķg┐╝æ]���Ż¼═§└ŽÄ¤æ¬(y©®ng)▀xō±└@Ą└╚źīW(xu©”)ąŻ▀Ć╩Ū▀xō±═©▀^ōĒöDĄ─Ą└┐┌╚źīW(xu©”)ąŻ?
(2)╚¶į┌═§└ŽÄ¤Ą╚╚╦Ą─ŠS│ųŽ┬����Ż¼ÄūĘųńŖ║¾ų╚ą“╗ųÅ═(f©┤)š²│Ż(├┐ĘųńŖ╚įėą3╚╦═©▀^Ą└┐┌)���Ż¼ĮY(ji©”)╣¹═§└ŽÄ¤▒╚ōĒöDĄ─ŪķørŽ┬╠ßŪ░┴╦6ĘųńŖ═©▀^Ą└┐┌�Ż¼å¢ŠS│ųų╚ą“Ą─Ģr(sh©¬)ķg╩ŪČÓ╔┘?
Ņ}ą═░╦Ż║┼õ╠ūå¢Ņ}
“┼õ╠ū”ą═æ¬(y©®ng)ė├Ņ}ųąėą╚²ĮMöĄ(sh©┤)ō■(j©┤)Ż║
(1)▄ćķg╣ż╚╦Ą─╚╦öĄ(sh©┤);
(2)├┐╚╦├┐╠ņŲĮŠ∙─▄╔·«a(ch©Żn)Ą─▓╗═¼Ą─┴Ń╝■öĄ(sh©┤);
(3)▓╗═¼┴Ń╝■Ą─┼õ╠ū▒╚.
(└¹ė├(1)(3)Ą├ĄĮĄ╚┴┐ĻP(gu©Īn)ŽĄ�����Ż¼śŗ(g©░u)įņĘĮ│╠)
ę╗░ŃĄžšf�Ż¼(2)Īó(3)ā╔éĆ(g©©)öĄ(sh©┤)ō■(j©┤)┐╔ęįŅA(y©┤)Ž╚ĮoČ©.└²╚ńŻ¼į┌Įo│÷(2)��Īó(3)ā╔ĮMöĄ(sh©┤)ō■(j©┤)Ą─╗∙ĄA(ch©│)╔Ž�Ż¼╚ń║╬┤_Č©▄ćķg╣ż╚╦╚╦öĄ(sh©┤)Ż¼╩╣å¢Ņ}ėąš¹öĄ(sh©┤)ĮŌ.
└²16Ż║─│▄ćķgėą28├¹╣ż╚╦���Ż¼╔·«a(ch©Żn)ę╗ĘN┬▌╦©║═┬▌─Ė����Ż¼├┐╚╦├┐╠ņŲĮŠ∙─▄╔·«a(ch©Żn)┬▌╦©12éĆ(g©©)╗“┬▌─Ė18éĆ(g©©)���Ż¼ę╗éĆ(g©©)┬▌╦©ę¬┼õā╔éĆ(g©©)┬▌─Ė.Ą┌ę╗╠ņ░▓┼┼14├¹╣ż╚╦╔·«a(ch©Żn)┬▌╦©�����Ż¼14├¹╣ż╚╦╔·«a(ch©Żn)┬▌─Ė���Ż¼å¢Ą┌Č■╠ņæ¬(y©®ng)Ęų┼õČÓ╔┘╚╦╔·«a(ch©Żn)┬▌╦©ĪóČÓ╔┘╚╦╔·«a(ch©Żn)┬▌─Ė�����Ż¼▓┼─▄╩╣ā╔╠ņ┐éĄ─╔·«a(ch©Żn)ą¦┬╩ūŅĖ▀?
└²17Ż║─│▄ćķgėą62éĆ(g©©)╣ż╚╦�Ż¼╔·«a(ch©Żn)╝ū����Īóęęā╔ĘN┴Ń╝■�����Ż¼├┐╚╦├┐╠ņŲĮŠ∙─▄╔·«a(ch©Żn)╝ūĘN┴Ń╝■12éĆ(g©©)╗“ęęĘN┴Ń╝■23éĆ(g©©).ęčų¬├┐3éĆ(g©©)╝ūĘN┴Ń╝■║═2éĆ(g©©)ęęĘN┴Ń╝■┼õ│╔ę╗╠ū��Ż¼å¢æ¬(y©®ng)Ęų┼õČÓ╔┘╚╦╔·«a(ch©Żn)╝ūĘN┴Ń╝■��Ż¼ČÓ╔┘╚╦╔·«a(ch©Żn)ęęĘN┴Ń╝■��Ż¼▓┼─▄╩╣├┐╠ņ╔·«a(ch©Żn)Ą─▀@ā╔ĘN┴Ń╝■äé║├┼õ╠ū?
Ņ}ą═Š┼Ż║ĘeĘųå¢Ņ}
▒╚┘Éł÷öĄ(sh©┤)=ä┘Ą─ł÷öĄ(sh©┤)+ŲĮĄ─ł÷öĄ(sh©┤)+žō(f©┤)Ą─ł÷öĄ(sh©┤)����Ż¼▒╚┘ÉĘų?j©½n)?sh©┤)=ä┘ł÷Ą├Ęų+ŲĮł÷Ą├Ęųžō(f©┤)ł÷┐█Ęų����ĪŻ
└²18Ż║ūŃŪ“▒╚┘ÉĄ─ėøĘųęÄ(gu©®)ät×ķŻ║ä┘ę╗ł÷Ą├3ĘųŻ¼ŲĮę╗ł÷Ą├1Ęų����Ż¼▌öę╗ł÷Ą├0Ęų.ę╗ų¦ūŃŪ“ĻĀ(du©¼)į┌─│éĆ(g©©)┘É╝Šųą╣▓ąĶ▒╚┘É14ł÷Ż¼¼F(xi©żn)ęč▒╚┘É┴╦8ł÷��Ż¼▌ö┴╦ę╗ł÷Ż¼Ą├17Ęų.
(1)Ū░8ł÷▒╚┘Éųą���Ż¼▀@ų¦Ū“ĻĀ(du©¼)╣▓ä┘┴╦ČÓ╔┘ł÷?
(2)▀@ų¦Ū“ĻĀ(du©¼)┤“ØM14ł÷▒╚┘É�����Ż¼ūŅĖ▀─▄Ą├ČÓ╔┘Ęų?
(3)═©▀^ī”▒╚┘ÉŪķørĄ─Ęų╬÷���Ż¼▀@ų¦Ū“ĻĀ(du©¼)┤“ØM14ł÷▒╚┘ÉŻ¼Ą├Ęų▓╗Ą═ė┌29Ęų����Ż¼Š═┐╔ęį▀_(d©ó)ĄĮŅA(y©┤)Ų┌─┐ś╦(bi©Īo).šł─ŃĘų╬÷ę╗Ž┬Ż¼į┌║¾├µĄ─6ł÷▒╚┘Éųą����Ż¼▀@ų¦Ū“ĻĀ(du©¼)ų┴╔┘ę¬ä┘Äūł÷Ż¼▓┼─▄▀_(d©ó)ĄĮŅA(y©┤)Ų┌─┐ś╦(bi©Īo).
ŠÄ▌ŗ═Ų╦]Ż║
2023─Ļųą┐╝Ė„┐Ų─┐ųž³c(di©Żn)ų¬ūRģR┐é
ĪĪĪĪūŅą┬ųą┐╝┘YėŹ���Īóųą┐╝š■▓▀��Īó┐╝Ū░£╩(zh©│n)éõ�����Īóųą┐╝ŅA(y©┤)£y�����Īóõø╚ĪĘų?j©½n)?sh©┤)ŠĆĄ╚
ĪĪĪĪųą┐╝Ģr(sh©¬)ķgŠĆĄ─╚½▓┐ųžę¬╣Ø(ji©”)³c(di©Żn)
ĪĪĪĪ▒Mį┌"ųą┐╝ŠW(w©Żng)"╬óą┼╣½▒Ŗ╠¢

ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC(j©®)��ĪóŲĮ░ÕĄ╚ęŲäėįO(sh©©)éõįLå¢ųą┐╝ŠW(w©Żng)��Ż¼2024ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą��ŻĪ>>³c(di©Żn)ō¶▓ķ┐┤












